Meta人工智能團隊早前開源了一個可微分非線性最小二乘（NLS）的優化技術庫Theseus。據介紹，Theseus基于PyTorch，適用于機器人和計算機視覺等用例，允許研究人員能夠輕松地將專家領域知識融入現代AI架構。它將knowledge表示為優化問題，并在基于梯度的學習過程中將其作為模塊化“優化層”添加到架構之中。這個domain knowledge與訓練數據不同，它可以幫助模型實現更為準確的預測。例如，為了確保機器人的運動平穩，研究人員可以將機器人的實現方式和運動模式的knowledge作為一個層，同時對機器人進行端到端的運動訓練。

Theseus是一個為可微非線性優化提供跨應用框架的庫。Theseus非常高效，可通過支持批處理、GPU加速、稀疏解算器和隱式微分來加速計算和內存。Meta宣稱，它比谷歌基于C++的Ceres Solver（不支持端到端學習）快四倍。

Theseus融合了將prior knowledge注入人工智能系統的兩種主流方法的最佳方面。在深度學習出現之前，研究人員使用更簡單、獨立的AI優化算法來解決機器人中的單個問題。通過計算手動選擇的因素組合的最小值，機器人系統學會了執行命令的最佳方式。這種方法有效但不靈活。特定于應用的優化算法通常難以適應新的系統或環境。

另一方面，深度學習方法的可擴展性要高得多，但它們需要大量的數據，會產生有效但在training domain之外脆弱的解決方案。

為了訓練特定應用的深度學習模型，研究人員使用精心選擇的損失函數來衡量模型預測數據的效果。但要通過反向傳播更新模型權重，每個層必須是可微分，允許誤差信息通過網絡流動。傳統的優化算法不是端到端可微分，所以研究人員面臨著一個權衡：他們可以放棄優化算法，轉而進行專門針對特定任務的端到端深度學習，并有可能失去優化的效率及其泛化能力。

或者，他們可以離線訓練深度學習模型，并在推理時將其添加到優化算法中。第二種方法的優勢是將深度學習和prior knowledge相結合，但由于深度學習模型是在沒有預存在信息或特定任務的錯誤函數的情況下訓練，所以其預測可能不準確。

為了融合相關策略，減輕它們的弱點并利用它們的優勢，Theseus將優化結果轉換為一個可以插入任何神經網絡架構的層。這樣，修改可以通過優化層反向傳播，從而允許研究人員對最終任務損失的特定domain knowledge進行微調，并作為端到端深度學習模型的一個組成環節。

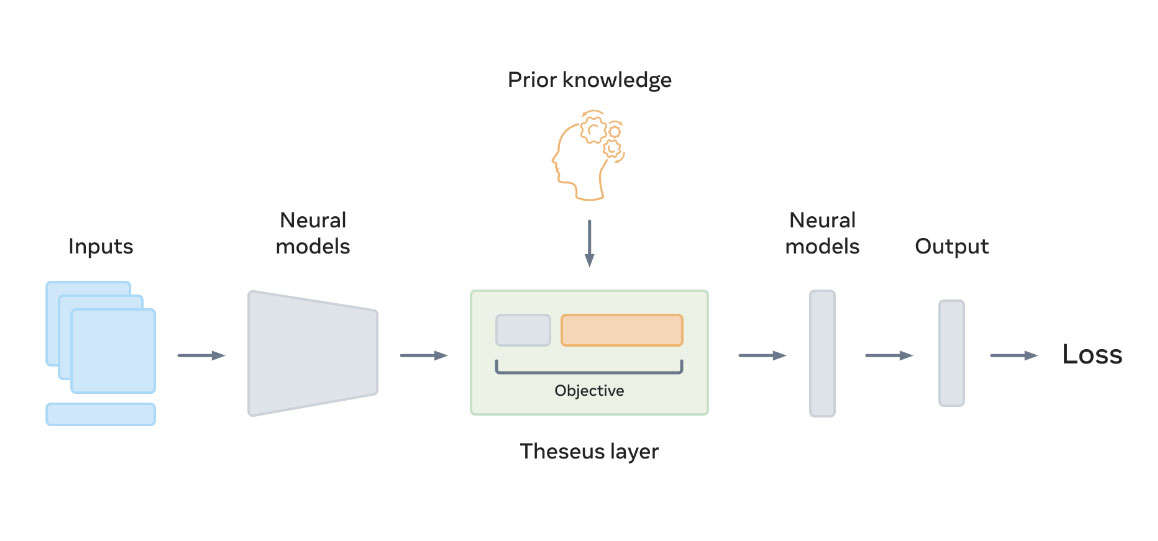
Theseus（綠色）如上所示， objective由上游神經模型的輸出張量（灰色）和prior knowledge（橙色）組成。Theseus層的輸出是最小化 objective的張量。

工作原理

NLS測量一個非線性函數與它要預測的實際數據之間的差異。較小的值意味著函數非常適合數據集。從映射和估計到規劃和控制，NLS在機器人和視覺問題的表述中非常普遍。例如，機器人朝向目標的路線可以表述為NLS優化問題：為了繪制最快的安全軌跡，系統會尋找一個可以最小化行程時間和不必要行為的sum-of-costs objective，比方說急轉彎或與環境中的障礙物碰撞。sum-of-costs objective同時可以捕獲傳感器測量誤差，從而優化機器人或camera的過去軌跡。

通過令NLS可微分，Theseus提供了可微非線性優化，并作為研究人員可以插入神經網絡的層。輸入張量定義了加權平方和objective函數，輸出張量是產生objective最小值的參數。通過優化器進行微分，可以保留端到端計算梯度的能力。

這將優化器和已知先驗集成到深度學習訓練循環中，允許模型對domain knowledge進行編碼，并學習實際的任務損失。同時，深度學習模型將從訓練過程中的感知或語言教學中提取更大的objective。這樣，研究人員可以在訓練循環中使用已知的運動學模型來開發objective預測模型。這種將已知先驗與神經組件模塊化混合的技術可以提高數據效率和泛化能力。

為了提高效率，Theseus集成了對稀疏解算器、自動矢量化、批處理、GPU加速和帶隱式微分的梯度計算的支持。正如autodiff和GPU加速推動了PyTorch在NumPy的發展一樣，稀疏性和隱式微分推動了Theseus的發展，與通常只支持稀疏性的Ceres等解算器形成對比。

對于標準GPU，使用稀疏解算器的Theseus要比使用密集解算器快得多，所需內存同樣要少得多。另外，Ceres的GPU支持有限，不支持分批或端到端學習。最后，隱式微分比標準展開產生更好的梯度。隱式差異同時具有恒定的內存和計算占用空間。

為何重要

Theseus提供了一個可以利用傳統技術、視覺方法和深度學習的互補優勢的通用框架。可微分優化作為歸納先驗，提高數據效率和泛化能力。

現有的實現是特定于任務，通常效率低下。Theseus可以跨應用，所以AI社區可以通過訓練在多個任務和環境中表現出色的精確模型來取得更快的進展。

相關論文：Theseus: A Library for Differentiable Nonlinear Optimization

Theseus目前已經開源。具體源代碼請訪問這里，而項目頁面請訪問這里。